Vlastník sbírky: Eva Kopcová

Řešení

Výsledky

Tisknout

Množiny bodů dané vlastnosti

www.SbirkaPrikladu.eu/s/63

1. Množina bodů dané vlastnosti

Zadání:

Je dána kružnice k(S, r = 4 cm). Najděte množinu všech středů kružnic o poloměru 2 cm, které se zvenku dotýkají kružnice k.

Řešení:

Výsledek:

Množinou je kružnice l(S, r = 6 cm).

2. Množina bodů dané vlastnosti

Zadání:

Je dán trojúhelník ABC, kde strana AB má délku 4 cm. Najděte množinu všech vrcholů C trojúhelníku ABC s obsahem 4 cm².

Řešení:

Výsledek:

Množinou je dvojice navzájem rovnoběžných přímek vzdálených 2 cm od strany AB.

3. Množina bodů dané vlastnosti

Zadání:

Jsou dány dvě soustředné kružnice k₁(S, r = 4 cm) a k₂(S, r = 6 cm). Najděte množinu všech středů kružnic, které se dotýkají obou kružnic k₁ a k₂.

Řešení:

Výsledek:

Množinou je kružnice l(S, r = 5 cm).

4. Množina bodů dané vlastnosti

Zadání:

Je dána úsečka AB délky 8 cm. Najděte množinu všech středů kosočtverců se stranou AB.

Řešení:

Výsledek:

Množinou je kružnice s průměrem AB kromě bodů A, B.

5. Množina bodů daných vlastnosti s využitím kružnice

Zadání:

Je dána kružnice k (S; r = 4cm) a bod A, přičemž platí

. Sestroj množinu všech bodů, které mají od kružnice k vzdálenost 2 cm a od bodu A vzdálenost 3 cm.

Řešení:

Postup konstrukce:

Výsledek:

Množinou bodů daných vlatností jsou dva body - X a Y

6. Množina bodů daných vlastností s využitím kružnice

Zadání:

Jsou dány body A, B a C, které neleží na jedné přímce. Sestroj množinu všech bodů, které mají od přímek AB a AC stejnou vzdálenost a od bodu B mají vzdálenost 4 cm.

Řešení:

Postup konstrukce:

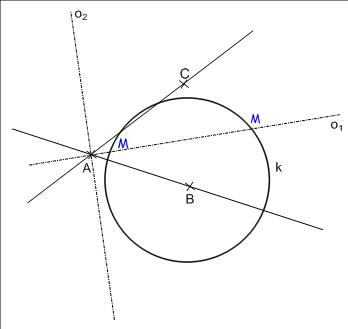
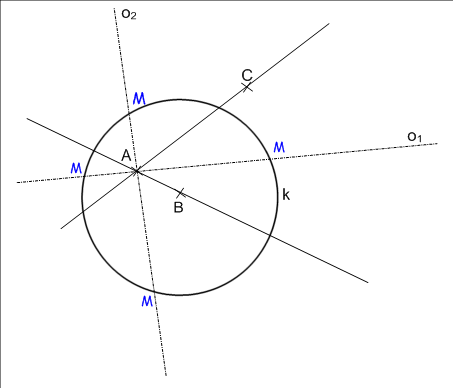
Množinu všech bodů, které mají od dvou různoběžných přímek AB a AC stejnou vzdálenost, jsou osy úhlů, které různoběžky svírají - jedná se o dvojici kolmých přímek. Druhou množinou bodů dle zadání je kružnice se středem v bodě B o poloměru 4 cm.

Výsledek:

1. varianta: Úloha má dvě řešení - body M

2. varianta: Úloha má 4 řešení - body M

7. Množina bodů daných vlastností

Zadání:

Jsou dány dvě různoběžné přímky p a q (ne navzájem kolmé). Sestroj množinu všech bodů, které mají od přímky p vzdálenost 5 cm a od přímky q vzdálenost 3 cm.

Řešení:

Postup konstrukce:

Výsledek:

Úloha má 4 řešení - body M.

8. Množina bodů daných vlastností

Zadání:

Jsou dány dvě kolmé přímky p a q. Sestroj množinu všech bodů, které mají od obou přímek vzdálenost 3 cm.

Řešení:

Postup konstrukce:

Výsledek:

Úloha má 4 řešení - body M

9. Množina bodů daných vlastnosti

Zadání:

Jsou dány dvě rovnoběžné přímky p a q, jejichž vzdálenost jsou 2 cm. Sestroj množinu všech bodů, které mají od přímky p vzdálenost 5 cm a od přímky q vzdálenost 3 cm

Řešení:

Postup konstrukce:

Výsledek:

Řešením úlohy jsou přímky

, které jsou totožné - nekonečné množství bodů M.

10. Množina bodů daných vlastností s využitím kružnice

Zadání:

Je dána kružnice k(S,6cm) a přímka p, jejíž vzdálenost od bodu S jsou 4 cm. Sestrojte množinu všech bodů, které mají od přímky p vzdálenost 2 cm a od kružnice k vzdálenost 4 cm

Řešení:

Postup konstrukce:

Výsledek:

Úloha má pět řešení - body X, Y, R, Z a S.

11. Množina bodů daných vlastností s využitím kružnice

Zadání:

Jsou dány body A a B,

. Sestroj množinu všech bodů, které mají od obou bodů stejnou vzdálenost.

Řešení:

Postup konstrukce:

Výsledek:

Množinou všech bodů je osa úsečky AB

12. Množina bodů dané vlastnost s využitím kružnice

Zadání:

Je dána přímka p a bod A. Vzdálenost bodu A od přímky p je 5 cm. Sestroj množinu všech bodů, které mají od bodu A vzdálenost 5 cm a od přímky p vzdálenost 4 cm.

Řešení:

Postup konstrukce:

Výsledek:

Úloha má dvě řešení - body X a Y

Kliknutím vyberte jména autorů jejichž příklady chete zobrazit

Tisk

Tiskový náhled sbírky vidíte na pozadí

Nastavte další parametry pro tisk:

Množiny bodů dané vlastnosti

1. Množina bodů dané vlastnosti

Zadání:

Řešení:

Výsledek:

2. Množina bodů dané vlastnosti

Zadání:

Řešení:

Výsledek:

3. Množina bodů dané vlastnosti

Zadání:

Řešení:

Výsledek:

4. Množina bodů dané vlastnosti

Zadání:

Řešení:

Výsledek:

5. Množina bodů daných vlastnosti s využitím kružnice

Zadání:

Řešení:

Výsledek:

6. Množina bodů daných vlastností s využitím kružnice

Zadání:

Řešení:

Výsledek:

7. Množina bodů daných vlastností

Zadání:

Řešení:

Výsledek:

8. Množina bodů daných vlastností

Zadání:

Řešení:

Výsledek:

9. Množina bodů daných vlastnosti

Zadání:

Řešení:

Výsledek:

10. Množina bodů daných vlastností s využitím kružnice

Zadání:

Řešení:

Výsledek:

11. Množina bodů daných vlastností s využitím kružnice

Zadání:

Řešení:

Výsledek:

12. Množina bodů dané vlastnost s využitím kružnice

Zadání:

Řešení:

Výsledek: